Резонанс токов

Для исследования явления резонанса токов соберем установку (рис. 1, а) из двух параллельно включенных ветвей R₁C- и R₂L- элементами, где R₁ - сопротивление реостата, R₂ - активное сопротивление катушки индуктивности.

Рис. 1.

При изменении емкости батареи конденсаторов наблюдается экстремальная зависимость суммарного тока I от емкости С₀. Но, в отличие от предыдущего, здесь при резонансе имеет место минимум тока. Такой режим называется резонансом токов. Для определения параметров электрической цепи (рис. 1, б), при которых ток совпадает по фазе с напряжением, приравняем к нулю суммарную реактивную проводимость цепи. Комплексные действующие значения тока в ветвях, согласно с законом Ома, составят:

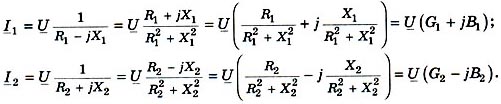
Ток в неразветвленной части цепи (рис. 1, в)

Если В₂ = В₁ = 0, ток  совпадает по фазе с напряжением. Если в уравнении В₁ = В₂ заменить реактивные проводимости, получим:

отсюда определим частоту резонанса:

Эта формула указывает, что для резонанса токов необходимо одновременное выполнение таких неравенств:

Иначе значение круговой частоты будет мнимым, т.е. не существует частот, при которых возможен резонанс токов. Однако, для одинаковых активных сопротивлений ветвей  круговая частота будет такой же, как и при резонансе напряжений в последовательной цепи, т.е. . При условии  резонансная круговая частота  может иметь произвольное значение. В такой цепи резонанс токов наблюдается при любой частоте источника напряжения. В таком случае эквивалентное сопротивление всей схемы

и не зависит от частоты.

В идеальном контуре, если R₁ = R₂ = 0, ток в неразветвленной части электрической цепи равняется нулю.