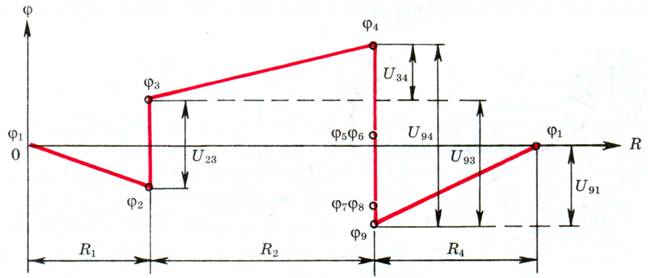
Потенциальная диаграмма
Заказать работу у нас! Решение онлайн! (New!)
Во время проектирования и эксплуатации электрических установок важно знать разность потенциалов между соответствующими точками схемы. Тогда элементы и узлы, имеющие существенную разность потенциалов, размещают территориально на большем расстоянии, чтобы предотвратить пробой изоляции между ними. Это особенно важно если имеются ограничения жесткими требованиями к габаритам. Для определения этой разности потенциалов строят в координатах «сопротивление ветвей - потенциалы» потенциальные диаграммы. Примем потенциал отрицательного полюса источника (см. рис. 1) нулевым.
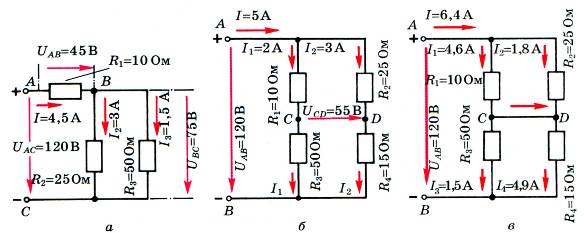
Рис. 1.
Тогда φА = 120 В. Когда движение направлено от точки А к точке В, потенциал будет уменьшаться на значение падения напряжения на сопротивлении участка. Например, для схемы (рис. 1, а) φС = φА – I2R2 . Если на горизонтальной оси откладывать последовательно сопротивление участков, обходя контур по часовой стрелке, а на вертикальной – потенциал точек, то для первой, второй и третьей схем соединения (рис. 1. а, б, в) получаем кусочно-линейные зависимости (рис. 2 а, б, в). Тангенсы углов наклона графика, с учетом масштабных коэффициентов осей сопротивлений (mR ) и потенциалов (mU), пропорциональны токам ветвей.
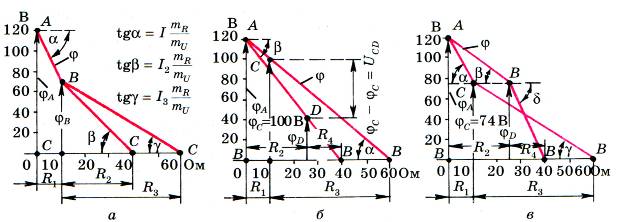
Рис. 2.
Для произвольного контура (рис. 3), зная токи, сопротивления, ЭДС ветвей, на основании закона Ома для активного участка цепи вычисляют потенциалы промежуточных точек. Затем строят потенциальную диаграмму. Согласно закона Ома, U12 = φ1 – φ2 – I1R1. Зададим условно нулевое значение потенциала φ1 точки 1 (узел 1 заземлен). Тогда φ2 = - I1R1 < 0. Двигаясь далее по контуру от узла 2 в узел 3, проходим идеальную ЭДС Е1. Напряжение U32 = φ3 – φ2 – Е1, откуда φ3 = φ2 + Е1 = Е1 - I1R1 . Для ветви 3 – 4 – 5 направление обхода контура противоположен току I, поэтому φ4 > φ3, или U43 = φ4 – φ3 = I2R2 > 0. Благодаря этому φ4 = φ3 + I2R2 = (Е1 - I1R1) + I2R2. Напряжение U54 = φ5 – φ4 = - Е2, откуда φ5 = φ4 - Е2. Ветвь 5 – 6 – 7 – 8 разорвана, ток I3 в ней отсутствует и U75 = U76 = U85 = φ8 – φ5, где φ5 уже определено, а U76 известно. Тогда φ8 = U76 + φ5. Для ветви 8 – 9 – 1: φ9 – φ8 = - Е3, или φ9 = φ8 - Е3 и φ1 – φ9 = + I4R4, что в соответствии с начальным условием должно быть равно нулю (условие проверки).
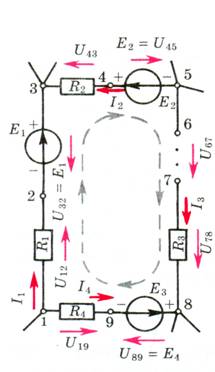
Рис. 3.
График распределения потенциала по контуру (рис. 4) дает представление о разности потенциалов между любыми двумя точками контура. Например, U49 = φ4 – φ9 максимальна, что учитывается при конструктивном внедрении схемы в конкретной установке. Необходимо обеспечить надежную электрическую изоляцию этих точек или разнести их в пространстве, чтобы не было электрического пробоя диэлектрика. Чем большее расстояние l между этими точками, тем меньшая напряженность электрического поля ε = U49/l.
Задачи по эконометрике смотрите здесь