Электрическая цепь синусоидального тока с индуктивностью

Соберем установку (рис. 1, а). Пусть внутренние активные сопротивления, источники напряжения (сети промышленной частоты 50 Гц с напряжением, действующее значение напряжения 120 В) и катушки индуктивности 95 мГн, равняются нулю. В схеме замещения (рис. 1, б) имеем цепь из идеальных источника напряжения и индуктивности L. В этот раз, кроме приборов, использованных с активным сопротивлением, дополнительно включен ваттметр для измерения, так называемой полной мощности (в данном случае реактивной Q_L), имеющей размерность "вольт-ампер-реактивный" (ВАР). Включим выключатель. Приборы показывают U = 120 В, I = 4 А, Р = 0,  Q_L = 480 ВАР. Если выразить сопротивление катушки как отношение U к I и обозначить его X_L, то X_L = 30 Ом. Поскольку активное сопротивление катушки равно нулю, то, очевидно, она имеет еще какое-то сопротивление, которое названо индуктивным. Иначе бы ток был неограниченно большим.

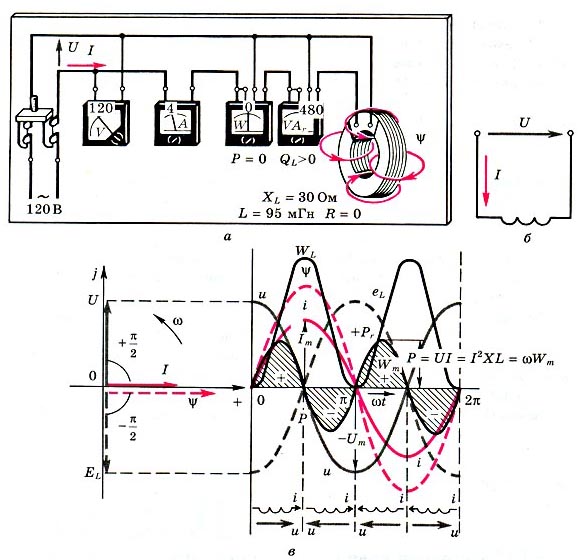
Рис. 1.

Противодействует этому ЭДС самоиндукции, которая возникает в катушке индуктивности при любом изменении в ней тока i(t) и по закону Ленца противодействует этому изменению. Если направления U(t) и i(t) принять одинаковыми, то знаки при e_L(t) и  всегда будут противоположными. Согласно второго закона Кирхгофа для цепи (рис. 1, б) напряжение U(t) источника уравновешивается ЭДС самоиндукции -e_L(t):

Тут может возникнуть вопрос: если U(t) + e_L(t) = 0, то откуда тогда берется ток i(t)? 
Для реальной катушки, которая имеет внутреннее активное сопротивление R,

,

где U(t) и e_L(t) - всегда противоположны.  Для идеальной катушки числитель и знаменатель указанного выше выражения стремятся к бесконечно малым значениям, поэтому их отношение, равное i(t) - величина фиксированная. Для построения диаграмм (рис. 1, в) примем начальную фазу , т.е. . Тогда напряжение U(t) и ЭДС e_L(t), составят:

Если  достаточно мало, то

То есть

где

или, для действующих значений,

.

Поскольку U имеет размерность Вольт, а I - Ампер, то их отношение - это модуль индуктивного сопротивления X_L:

Для установки (рис. 1, а) .
Символический метод описания синусоидальных функций:

На комплексной плоскости (рис. 1, в): вектор  совпадает с действительной осью, вектор  опережает, а вектор  отстает от вектора тока  на угол . Отношение комплексов напряжения к току дает комплексное (индуктивное )сопротивление

Индуктивное сопротивление пропорционально частоте w и индуктивности L.
В схеме есть ток 4 А, сопротивление 30 Ом, а ваттметр активной мощности показывает ноль. Почему так? Активная мощность Р равняется среднему за период значению мгновенной мощности. Мгновенная мощность:

Активная мощность - среднее за период значение (заштрихована на рис 1, в синусоида двойной частоты) равняется нулю: в первую четверть периода ток и напряжение совпадают по направлению, магнитное поле (потокосцепление ) возрастает, происходит превращение электрической энергии источника в магнитную - потребителя; во вторую четверть - напряжение и ток имеют противоположные направления, энергия магнитного поля Li²/2 уменьшается, поскольку катушка отдает ее источнику; далее все повторяется. Энергия W_L магнитного поля катушки (рис. 1, в) имеет пульсирующий характер: то накапливается до максимума, то спадает до нуля (в отличие от энергии W_R). Амплитуду колебаний мгновенной мощности называют реактивной мощностью Q, в данном случае индуктивной Q_L. В установке (рис.1, а) она составляет 480 ВАР, что совпадает с произведением U на I. 
Закон Ома для электрической цепи синусоидального тока с индуктивностью:

где комплекс  напряжения пропорционален комплексу  тока. Коэффициент пропорциональности - индуктивное сопротивление.