Расчет линейной электрической цепи однофазного синусоидального тока
Для цепи, изображенной на рис. 1 требуется:
- Определить комплексным методом действующие значения напряжений и токов на всех участках цепи.
- Определить активные, реактивные и полные мощности каждого участка цепи и всей цепи.
- Составить баланс активных и реактивных мощностей и оценить погрешность расчета.
- Построить векторную диаграмму токов и напряжений.
Частота питающего напряжения 50 Гц.
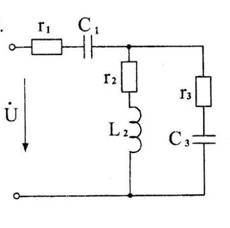
Рис. 1
Исходные данные:
U = 127 В , r1 = 15 Ом , C1 = 60 мкФ, r2 = 10 Ом , L2 = 80 мГн, r3 = 15 Ом , C3 = 90 мкФ.
Решение. Заказать у нас работу! Решить онлайн! (New!!!)
- Определим комплексные сопротивления каждой ветви.
![]() (Ом)
(Ом)
![]() (Ом)
(Ом)
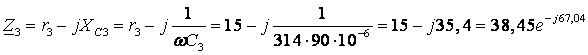 (Ом)
(Ом)
2. Определим полное сопротивление цепи.
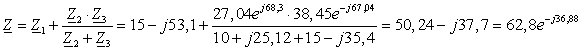 (Ом)
(Ом)
3. Приняв ![]() найдем токи и напряжения в ветвях.
найдем токи и напряжения в ветвях.
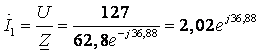 (А)
(А)
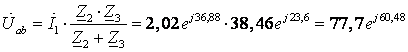 (В)
(В)
![]() (В)
(В)
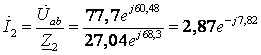 (А)
(А)
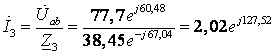 (А)
(А)
4. Определим активные, реактивные и полные мощности участков цепи и всей цепи целиком.
Мощность первого участка:
![]() (ВА)
(ВА)
Мощность второго участка:
![]() (ВА)
(ВА)
Мощность третьего участка:
![]() (ВА)
(ВА)
Полная мощность всей цепи:
![]() (ВА)
(ВА)
Проверим баланс активных мощностей:
P = P1 + P2 + P3
P = 205,2 (BA)
P1 + P2 + P3 = 61,25 + 82,44 + 61,22 = 204,91 (Вт)
Абс. погр-ть Δ = P – (P1 + P2 + P3) = 205,2 – 204,91 = 0,29 (Bт)
Отн. погр-ть ![]()
Проверим баланс реактивных мощноcтей:
S = S1 + S2 + S3
S =- 153,96 (BA)
S1 + S2 + S3 = - 216,7 + 207,19 – 144,5 = - 154,01 (ВА)
Абс. погр-ть Δ = |S – (S1 + S2 + S3)| = |153,96 – 154,01| = 0,05 (BA)
Отн. погр-ть ![]()
5. Построим векторную диаграмму на комплексной плоскости.
Для этого определим напряжения на каждом элементе схемы.
![]() (В)
(В)
![]() (В)
(В)
![]() (В)
(В)
![]() (В)
(В)
![]() (В)
(В)
![]() (В)
(В)
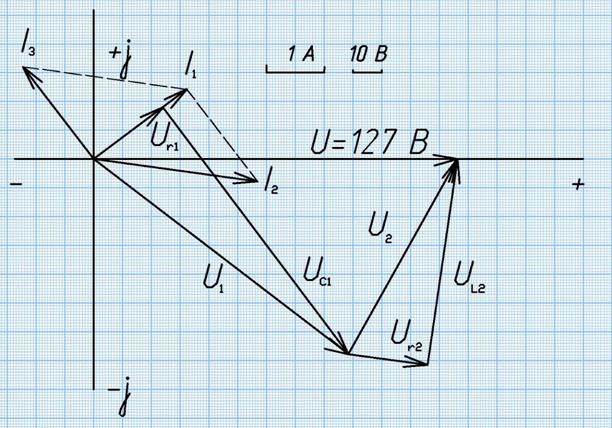
Рис. 2. Векторная диаграмма.


