Расчет электрических цепей методом узловых потенциалов

Из m уравнений системы можно получить n-1 уравнений узловых потенциалов, если воспользоваться уравнениями первого закона Кирхгофа и понятием проводимости.
Потенциалы узлов схемы считаются независимыми переменными. Один из них принимается равным нулю. Метод целесообразно использовать, когда (n-1)<(m-(n-1)). Количество узлов можно уменьшить (рис 1.), если заменить источник тока (рис 1, а) и параллельную ему ветвь эквивалентным реальным источником напряжения (рис 1, б).
Рассмотрим уравнения метода, используя неупрощенную схему (рис 1, а).

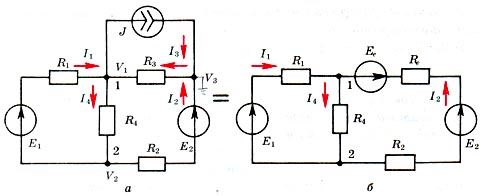
Рис. 1

Смотрите также: 
 Пример решения конкретной задачи методом узловых потенциалов № 1
 Пример решения конкретной задачи методом узловых потенциалов № 2
 Пример решения конкретной задачи методом узловых потенциалов № 3
 Смотреть видео: Метод узловых потенциалов 2  (пример решения конкретной задачи) 

Пусть 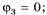 токи 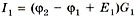 (принимаем направление тока от большего потенциала к меньшему, поэтому );

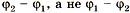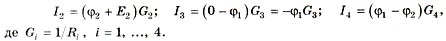
Подставив эти выражения в два первых уравнения Кирхгофа, будем иметь:

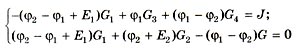
или относительно 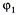 и :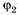

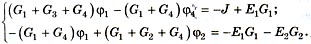
Уравнения в общем (стандартном для метода) виде запишем таким образом:

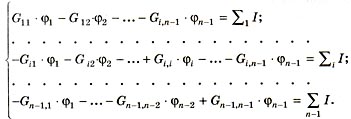
G_ii равняется сумме проводимостей ветвей, которые присоединены к i-му узлу; G_iJ равняется сумме проводимостей ветвей, которые соединяют i-й и j-й узлы; i, j = 1,..., n - 1.
Правые части равняются алгебраической сумме ЭДС, умноженной на проводимость ветвей, которые присоединены к узлу; ЭДС входят в уравнение со знаком "+", если направлены к узлу, со знаком "-", если направлены от узла; ток J источника переходит из левой в правую часть уравнения с обратным знаком (в нашем случае от узла J - со знаком "-"); если i-й и j-й узлы не связаны, то G_ij = 0; если в i-м узле нет ветвей с ЭДС или источниками тока, то (знак суммы)I = 0. 

Алгоритм метода узловых потенциалов:
1. Пронумеровать узлы схемы, приняв 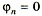 для n - го узла.
2. Задаться направлениями токов.
3. Записать и решить относительно (фи) систему уравнений.
4. На основании закона Ома, по найденным потенциалам и заданными проводимостями, найти токи в ветвях.

Для схемы (рис 1, б) после предварительного преобразования, приняв 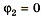, вместо двух получим одно уравнение:

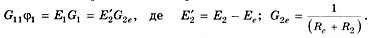
Отсюда

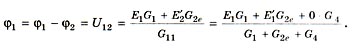
Это выражение в общей форме известно как формула двух узлов:

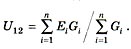
Она используется для вычисления напряжения U₁₂ на выходе n параллельно включенных источников ЭДС.