Трехпроводная трехфазная система звезда - звезда

Для симметричной нагрузки нет необходимости в использовании нейтрального провода. Система из четырехпроводной становится  трехпроводной (рис. 1).

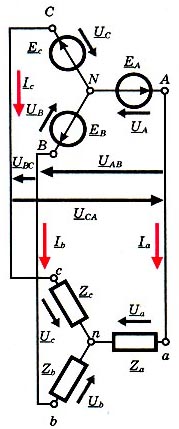
Рис. 1.

Симметрию имеют двигатели, трансформаторы и другие промышленные установки. Токи трехпроводной системы при симметричном нагружении не отличается от токов в четырехпроводной системе. Расчет сделаем для одной фазы.

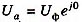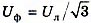Например, для фаза А напряжение , где , ток 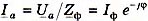. Диаграммы напряжений и токов аналогичны четырехпроводной системе. Если сопротивления фаз разные, симметрия напряжений и токов нарушается. Линейные напряжения системы не изменяются, если источник ЭДС идеальный (генератор большой мощности), но потенциал нейтральной точки потребителя уже не равен нулю. Его можно определить методом узловых потенциалов для двух узлов (n и N) в комплексной форме. 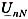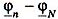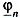Напряжение  смещения нейтрали равняется , или  при :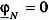

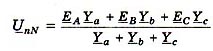
где 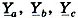 - комплексные проводимости фаз потребителя. Фазные напряжения потребителя также не равны фазным напряжениям напряжениям генератора:

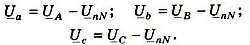
токи в фазах и в линии определяют по закону Ома.

Топографическая и векторная диаграммы напряжений и токов для потребителя имеют особенность. Поскольку 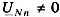, то нейтральная точка потребителя n не совпадает с нейтральной точкой генератора. Симметрия фазных напряжений нарушается. При изменении нагрузки в одной из фаз фазное напряжение изменяется не только в этой, но и в других фазах. Векторы токов на векторной диаграмме строят с учетом сопротивлений фаз потребителя.

Несимметричный режим возникает, например, в четырехпроводной ситсеме (рис. 2) в случае обрыва нейтрального провода (рис. 3).

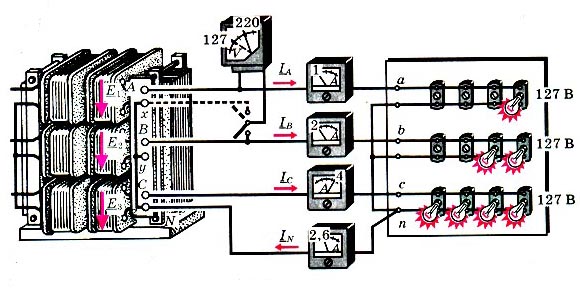
Рис. 2.

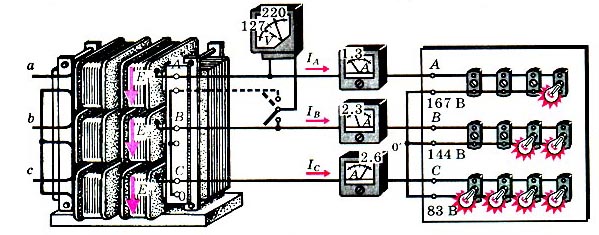
Рис. 3.

Чтобы определить напряжения и токи несимметричной нагрузки, рассчитывают сначала напряжение нейтрали. 

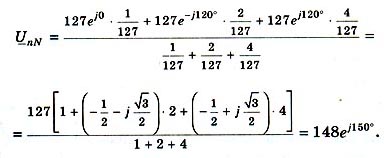
Напряжения определяют по второму закону Кирхгофа или графически, если построить векторно-топографическую диаграмму. Токи определяют, разделив напряжения на комплексные сопротивления соответствующих фаз. Ток 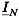 равняется геометрической сумме токов в фазах потребителя.

В случае обрыва провода в фаза А (рис. 4) и отсутствия нейтрального провода для симметричной нагрузки в фазах В и С смещение нейтрали, составит:

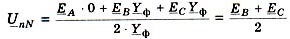
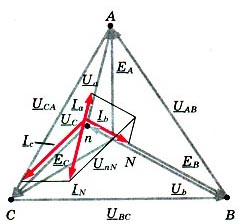
Рис. 4.

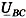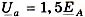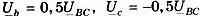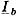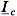Точка n лежит на середине вектора  (рис. 5), напряжения , , а токи  и  в 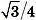 раз меньшие в сравнении с номинальными. 

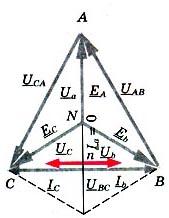
Рис. 5.

В случае короткого замыкания фазы А 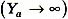 в отсутствие нейтрального провода Y_N = 0  и любой нагрузке в фазах В и С смещение нейтрали равняется Е_А. 

Потенциал точки n совпадает с потенциалом точки А (рис. 6), а напряжения равняются : , .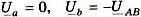 

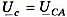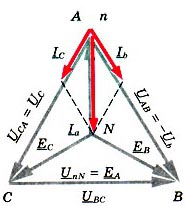
Рис. 6.

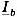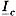Токи  и  в 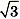 раз превышают номинальные, а ток  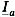в 3 раза больше номинального. На рис. 6 приведены векторы токов для активной нагрузки фаз В и С. 

Если в фазы В и С включить соответственно индуктивность и емкость, такие чтобы проводимости B_L = B_C = B, а в фазу А переменное активное сопротивление R (рис. 7), то при изменении сопротивления R от 0 до бесконечности (активная проводимость G изменяется при этом от  до 0) напряжение смещения нейтрали изменяется от 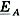 (как в случае короткого замыкания фазы А) до -, двигаясь вдоль действительной оси (рис. 8):

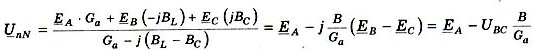
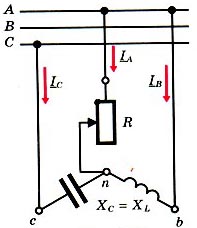
Рис. 7.

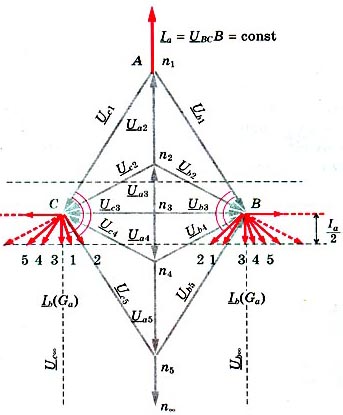
Рис. 8.

Когда G_a стремится к ,  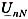стремится к  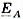; когда 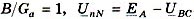, точка n  лежит на середине вектора  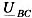аналогично режиму обрыва провода в фазе А. При дальнейшем увеличении соотношения В/G_a (уменьшении G_a) смещение  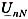продолжает расти по модулю, увеличиваются фазные напряжения  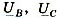и токи 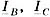. При приближении G_a к нулю токи и напряжение фаз В и С возрастают до бесконечности. Ток  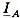при изменении G_a остается неизменным:

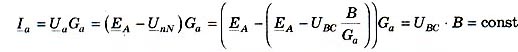
На рис. 8 приведены линейные годографы изменения токов и напряжений в функции G_a. Таким образом, в трехфазной RLC-нагрузке, включенной по схеме "звезда", при выполнении условия резонанса (B_L = B_C) сопротивление R (проводимость G_a) определяет добротность резонансного контура.

Здесь (в отличие от последовательно включенных RLC-элементов, где добротность обратно пропорциональна R) добротность прямо пропорциональна R, как в цепи с параллельно соединенными RLC-элементами.