Комплексный метод описания синусоидальных электрических величин

На горизонтальной оси координат комплексной плоскости отмечают действительный части комплексных чисел, на вертикальной - мнимые. Первая из них обозначается знаком "плюс" или буквами Re (relative - реальный, действительный); вторая буквами j или Im (imenginame - мнимый). Комплексное число 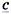 на комплексной плоскости изображается точкой или вектором с двумя координатами (a, jb):

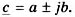
Черточкой внизу обозначаются комплексные числа, 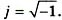 Так синусоиду, которая изображена на рис. 1 вектором 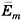, который вращается со скоростью  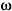радиан в секунду и в момент времени t = 0 имеет начальную фазу 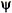, выражается комплексом 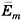, который имеет два компонента: действительную часть  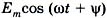и мнимую часть :

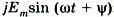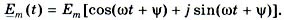(1)

 

 

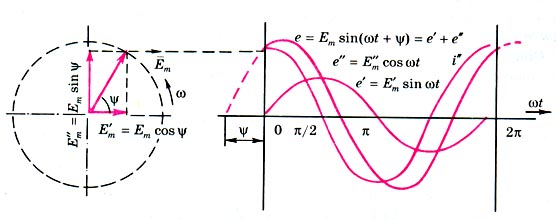
Рис. 1.

Эта же запись по формуле Эйлера, связывающей тригонометрическую и показательную формы чисел:

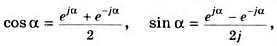 (2)

таким образом получаем более простое выражение. Подставим (2) в (1), когда :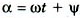

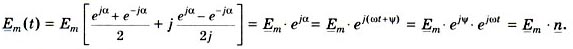
Комплекс 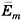 (рис. 2, а) называется символической формой изображения комплекса  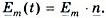Комплекс  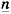- это единичный радиус-вектор, который вращается со скоростью  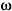и имеет нулевую начальную фазу (рис. 2, б):

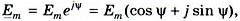 (3)

 (4)

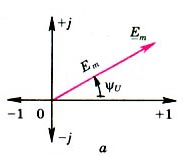
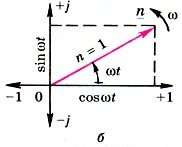
Рис. 2.

Во время линейных превращений вектор 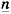 будет присутствовать во всех частях. Его можно вынести за скобки и расчеты проводить только для символьных частей  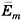комплексов 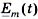. Например, сложим две синусоиды

,

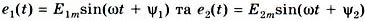пользуясь комплексным методом:

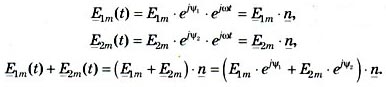
Чтобы сложить два символьных комплекса, которые в скобках, нужно перевести их из показательной формы 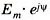 в алгебраическую. Между ними существует зависимость:

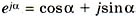. (5)

Таким образом,

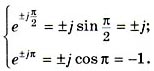
Тогда

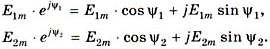
Чтобы сложить (вычесть) два комплексных числа, необходимо отдельно сложить (вычесть) их действительные части и мнимые части:

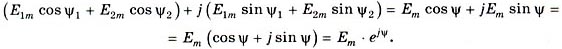
Умножив полученное значение символьного вектора 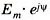 на единичный вектор 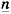, получим выражение для суммы двух синусоид, выраженных комплексам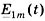и  и 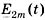. Мгновенное значение e(t) определяемой суммы равняется мнимой части (Im) вектора :

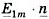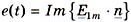
или

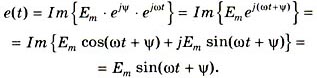
Комплексы одной частоты вращаются относительно неподвижной плоскости (рис. 3, а) с одинаковыми угловыми скоростями 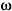. Их взаимное расположение остается неизменным. Можно считать, что эти векторы неподвижны, а плоскость вращается со скоростью  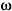(рис. 3, б). Тогда все расчеты выполняют символическим методом с символической (неизменной) частью  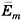комплексов  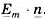Переход к временным функциям выполняют по формуле (5).

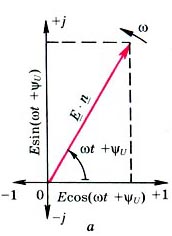
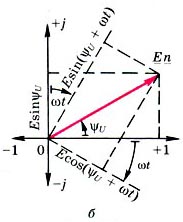
Рис. 3.

Энергетической моделью синусоидального тока, напряжения, ЭДС является действующее значение. Т.е. такие значения постоянного тока I, напряжения U, ЭДС, которые (согласно закона Джоуля-Ленца) приводят к выделению теплоты в сопротивлении R так же, как и соответствующие синусоидальные токи, напряжения, ЭДС.

Энергия, которая потребляется сопротивлением R за период T, для синусоидального тока равняется площади под кривой (рис. 4, в):

,

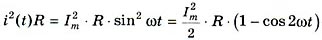которая взята за период Т.

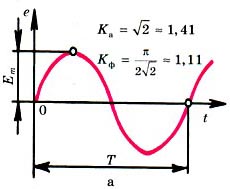
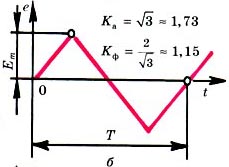
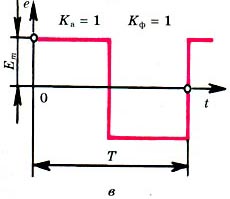
Рис. 4.

Поскольку cos2wt функция симметричная, то ее площади с "плюсом" и с "минусом" взаимо сокращаются. Тогда энергия за период, которая выделится на сопротивлении R при синусоидальном токе, составит 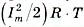 и по условию эквивалентности будет равняться энергии I²RT постоянного тока. Отсюда имеем соотношение:

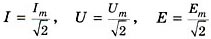
Во время расчетов, кроме амплитудных, пользуются скалярными I, U, E и векторными 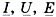 действующими значениями. Для анализа устройств выпрямления важны средние по полупериоду значения тока, ЭДС и напряжения:

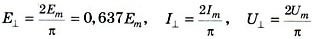
Отклонения формы периодической электрической величины от синусоиды выражают коэффициентом амплитуды К_а и формы К_ф:

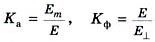
Временные диаграммы периодических ЭДС приведены на рис. 4 а - синусоидальной; б - треугольной; в - прямоугольной. Для синусоиды

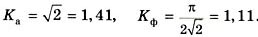
Для электрических величин кривые, которые имеют более острую форму, чем синусоида, коэффициенты составляют К_а > 1,41 и К_ф < 1,11. Для кривых более плоской формы К_а < 1,41 и К_ф > 1,11(рис. 4, б, в). Отклонения значений коэффициентов К_а и К_ф от 1,41 и 1,11 регистрируется по показаниям электроизмерительных приборов амплитудных, действующих и средних значений.