Второй закон Кирхгофа

«Обойдем» любой контур в любой схеме, например контур ACDBA в схеме (рис. 1, б).
 
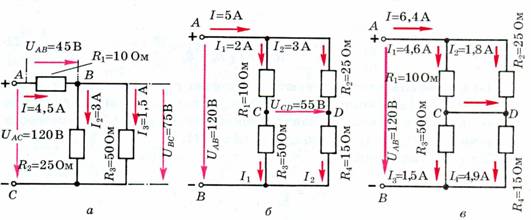
Рис. 1.

Смотрите еще:
 Пример решения задачи по правилам Кирхгофа № 1
 Пример решения задачи по правилам Кирхгофа № 2
 Пример решения задачи по правилам Кирхгофа № 3


В той же самой схеме контур ADCBA:

В общем случае (рис. 2) для контура в разветвленной цепи определим разность потенциалов между отдельными точками цепи:

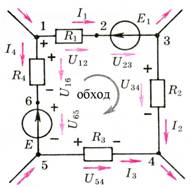
Рис. 2.
Добавив эти уравнения, получим, что:

или

В этом уравнении со знаком «плюс» берутся те ЭДС, где направление действия сторонних сил (внутренняя стрелочка) совпадает с направлением обхода контура, и со знаком «минус» - в противоположном случае; падение напряжения I·R имеет положительное значение, если направление тока и обхода совпадают, и со знаком «минус», когда ток направлен навстречу.
Если учесть, что ЭДС на идеальной части источника равняется соответствующему напряжению , то, согласно с указанным выше, имеем, что:

Т.е. алгебраическая сумма всех напряжений в контуре равняется нулю. Обобщив это, получим второй закон Кирхгофа:

или

Таким образом, алгебраическая сумма ЭДС всех веток контура и падение напряжений на сопротивлениях ветвей одинаковы, или алгебраическая сумма напряжений в контуре равняется нулю.
Напомним, что под контуром понимают замкнутый путь обхода вдоль ветвей цепи (рис. 3)

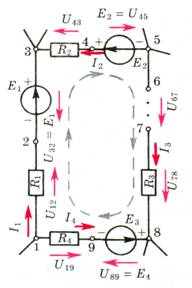
Рис. 3.
Не следует путать с замкнутой цепью, как замкнутым путем прохождения тока (рис. 2). Уравнение справедливо как для цепи (рис. 3), где ветвь 5 – 8 разорвана кА для тока, так и для цепи (рис. 2), где все ветви замкнуты.
Второй закон Кирхгофа, как и первый справедлив для постоянных и переменных во времени величин E, U, I, R; для линейных и нелинейных цепей; для мгновенных значений во времени E, U, I и других их изображений, однозначно связанных с ними (например при векторном отображении синусоидальных величин).