Задание. Расчет разветвленной электрической цепи постоянного тока

 

Дана электрическая цепь постоянного тока (рис. 1), параметры которой приведены в табл. 1.

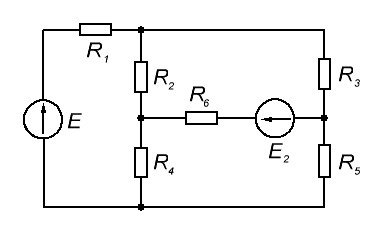
Рисунок 1

 

Требуется:

1. Определить токи во всех ветвях методом контурных токов.

2. Определить ток в одном из сопротивлений цепи, указанном в последнем столбце табл. 1, методом эквивалентного источника.

3. Построить график изменения потенциала (потенциальную диаграмму) по внешнему контуру.

4. Составить баланс мощностей.

Вар. 11

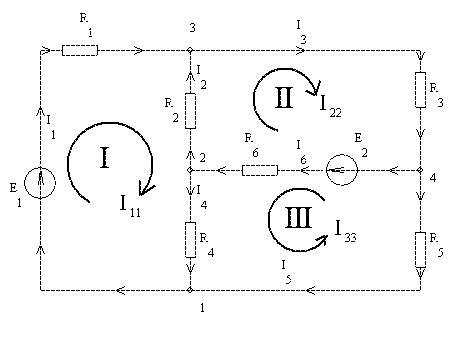
Электрическая схема

Исходные данные

R1=0,6Ом; R2=10,9Ом; R3=6Ом; R4=13,32Ом; R5=10,7Ом; R6=0,48Ом;

E1=21,6В; E2=2,83В;

 

Правила Кирхгоффа:

Решение

Запишем первое правило Кирхгоффа для узлов:

Узел 1: I1-I4-I5=0

Узел 1: I2+I4-I6=0

Узел 1: -I1-I2+I3=0

 

Запишем второе правило Кирхгоффа для контуров:

Контур I: -I2•R2+I4•R4+I1•R1=E1

Контур II: I3•R3+I6•R6+I2•R2=E2

Контур III: I4•R4-I5•R5+I6•R6=E2

 

Подставим числовые данные:

I1-I4-I5=0

I2+I4-I6=0

-I1-I2+I3=0

 

0,6I1-10,9I2+13,32I4=21,6

10,9I2+6I3+0,48I6=2,83

13,32I4-10,7I5+0,48I6=2,83

 

Решением этой системы уравнений будут следующие значения токов в ветвях:

I1=2,099 A

I2=-0,591 A

I3=1,508 A

I4=1,044 A

I5=1,055 A

I6=0,453 A

 

Метод контурных токов:

 

Решение

Запишем контурные уравнения:

Контур I: I11•R11+I22•R12+I33•R13=E11

Контур II: I11•R21+I22•R22+I33•R23=E22

Контур III: I11•R31+I22•R32+I33•R33=E33

 

где сопротивления контуров:

R11=R2+R4+R1=24,82 Ом

R12=-R2=-10,9 Ом

R13=R4=13,32 Ом

R21=-R2=-10,9 Ом

R22=R3+R6+R2=17,38 Ом

R23=R6=0,48 Ом

R31=R4=13,32 Ом

R32=R6=0,48 Ом

R33=R4+R5+R6=24,5 Ом

 

ЭДС в контурах:

E11= E1=21,6 В

E22= E2=2,83 В

E33= E2=2,83 В

 

Подставим числовые значения:

24,82I11-10,9I22+13,32I33=21,6

-10,9I11+17,38I22+0,48I33=2,83

13,32I11+0,48I22+24,5I33=2,83

 

Решением этой системы будут следующие значения контурных токов:

I11=2,098958 А

I22=1,508 А

I33=-1,0552 А

 

Отсюда токи в ветвях:

I1= I11=2,099 А

I2=-I11+I22=-0,591 А

I3= I22=1,508 А

I4= I11+I33=1,044 А

I5=-I33=1,0552 А

I6= I22+I33=0,45 А

 

И так далее …)))