Метод контурных токов
 Пример решения задачи методом контурных токов Решить онлайн! (New!!!)
Пример решения задачи методом контурных токов Решить онлайн! (New!!!)
Контурные токи – это условно независимые, одинаковые для всех ветвей каждого контура токи (рис.1 , указанные пунктиром II , III), которые совпадают по модулю с соответствующими токами внешних ветвей (например, ![]() ), токи смежных ветвей равняются их сумме (если, направления контурных токов совпадают) или разности (если направления противоположны). Например,
), токи смежных ветвей равняются их сумме (если, направления контурных токов совпадают) или разности (если направления противоположны). Например, ![]() .
.
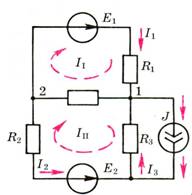
Рис.1.
Смотрите также
 Пример решения схемы методом контурных токов № 1
Пример решения схемы методом контурных токов № 1
 Пример решения схемы методом контурных токов № 2
Пример решения схемы методом контурных токов № 2
 Пример решения схемы методом контурных токов № 3
Пример решения схемы методом контурных токов № 3
 Пример решения схемы методом контурных токов № 4
Пример решения схемы методом контурных токов № 4
 Пример решения схемы методом контурных токов № 5
Пример решения схемы методом контурных токов № 5
Введение контурных токов дает возможность исключить из системы по первому и второму законам Кирхгофа уравнения первого закона Кирхгофа, снизив размерность системы до m – (n – 1). Для схемы (рис.1) исключим I3 и I4 из двух первых уравнений системы:
![]()
Из второго уравнения найдем I4, из первого – I3:
![]()
Подставим полученную формулу в два последних уравнения системы Кирхгофа:
![]()
Или относительно неизвестных I1 и I2:
![]()
После введения обозначений
![]()
(второе уравнение умножили на -1, чтобы III имел дополнительное значение) получим систему уравнений для контурных токов II и III:
![]()
где R12 = R21 = R4 (взаимное сопротивление Rij будет иметь отрицательное значение, если II и III направлены навстречу друг другу); Е2 также отрицательна, поскольку направление Е2, противоположно по направлению току III, должно быть в левой части уравнения со знаком «-» но после перехода вправо получило знак «+».
Обобщим систему для произвольного числа контуров:
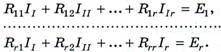
Элементы ![]() формируются согласно алгоритма метода контурных токов:
формируются согласно алгоритма метода контурных токов:
1. Выделить m – (n – 1) независимых контуров (каждый новый контур необходимо выбрать так, чтобы в него входил хотя бы один элемент электрической цепи, который не входит в другие контуры: например, для рис. 2, если выбраны контуры abd и bcd, то нельзя брать третьим контур abcd.
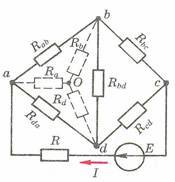
Рис.2.
2. Указать произвольно направления обхода контуров. Если на схеме уже обозначено направление токов в ветвях, то удобно направления контурных токов согласовать с направлением токов в ветвях.
3. Вычислить Rij: Rij равняется сумме сопротивлений всех элементов, входящих в i-й контур; Rij – равняется по модулю сумме сопротивлений ветвей, которые одновременно принадлежат i-му и j-му контурам; Rij больше нуля, если контурные токи i-го контура совпадают по направлению, и меньше нуля – при противоположных направлениях.
4. Вычислить правые части системы: Еi равняется алгебраической сумме ЭДС i-го контура; со знаком «+» берутся ЭДС, внутренняя стрелочка которых совпадает с направлением контурного тока i-го контура, «-» - если не совпадают. Если в семе есть источник тока J, то для его учета необходимо заблаговременно распределить ток J по ветвям любого незамкнутого контура, который дополняет ветвь с источником тока до замкнутого контура (в нашем случае – через R3, однако можно было бы и через R2 и R4). Полученное таким образом произведение J на соответствующее сопротивление необходимо перенести вправо, при этом необходимо поменять знак.
5. Решить систему уравнений относительно I. По контурным токам определить токи в ветвях. Во внешних ветвях они по модулю совпадают, во внутренних совпадающие по направлению складываются, направлены встречно – вычитаются. (В нашем примере I1 = I2; III = - I2; I1 – III = I4; ток I3 определим по первому закону Кирхгофа для узла 3: III – J + I3 = 0, откуда I3 = J - III).


