Расчет разветвленной линейной электрической цепи постоянного тока с несколькими источниками электрической энергии
Скачайте приложение для онлайн решения разветвленной цепи. Вам потребуется только нарисовать схему в редакторе программы и задать численные значения элементов.
Программа сама выдаст подробное пошаговое решение как если бы вы сами делали это РГР.
Для электрической цепи рис. 1, выполнить следующее:
- Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа. Решать эту систему уравнений не следует.
- Определить токи в ветвях методом контурных токов.
- Построить потенциальную диаграмму для любого замкнутого контура, содержащего обе ЭДС.
- Определить режимы работы активных элементов и составить баланс мощностей.
Значения ЭДС источников и сопротивлений приемников:
E1 = 130 В, Е2 = 110 В, R1 = 4 Ом, R2 = 8 Ом, R3 = 21 Ом, R4 = 16 Ом, R5 = 19 Ом, R6 = 16 Ом.
Смотрите также
 Пример решения схемы методом контурных токов № 1
Пример решения схемы методом контурных токов № 1
 Пример решения схемы методом контурных токов № 2
Пример решения схемы методом контурных токов № 2
 Пример решения схемы методом контурных токов № 3
Пример решения схемы методом контурных токов № 3
 Пример решения схемы методом контурных токов № 4
Пример решения схемы методом контурных токов № 4
 Пример решения схемы методом контурных токов № 5
Пример решения схемы методом контурных токов № 5
 Посмотреть видео "Метод контурных токов 2" (пример решения конкретной задачи)
Посмотреть видео "Метод контурных токов 2" (пример решения конкретной задачи)
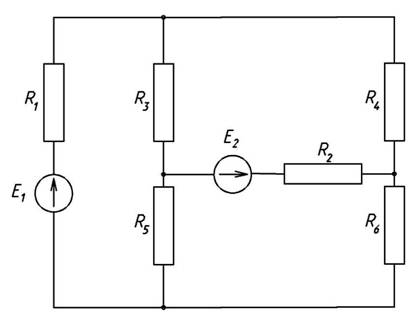
Рис. 1. Схема
Решение. Заказать работу! Решить онлайн! (New!!!)
1. Произвольно расставим направления токов в ветвях цепи, примем направления обхода контуров (против часовой стрелки), обозначим узлы.
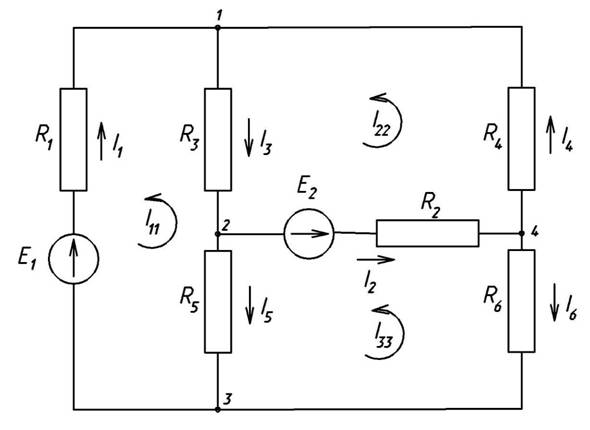
Рис. 2
2. Для получения системы уравнений по законам Кирхгофа для расчета токов в ветвях цепи составим по 1-му закону Кирхгофа 3 уравнения (на 1 меньше числа узлов в цепи) для узлов 1,2,3:
![]()
![]()
![]()
По второму закону Кирхгофа составим m – (р – 1) уравнений (где m – кол-во ветвей, р – кол-во узлов ), т.е. 6 – (4 – 1) = 3 для контуров I11, I22, I33:
![]()
![]()
![]()
Токи и напряжения совпадающие с принятым направлением обхода с «+», несовпадающие с «-».
Т.е. полная система уравнений для нашей цепи, составленная по законам Кирхгофа:
![]()
![]()
![]()
![]()
![]()
![]()
3. Определим токи в ветвях методом контурных токов. Зададимся направлениями течения контурных токов в каждом контуре схемы и обозначим их I11, I22, I33 (см. рис. 2)
4. Определим собственные сопротивления трех контуров нашей цепи, а так же взаимное сопротивление контуров:
![]() (Ом)
(Ом)
![]() (Ом)
(Ом)
![]() (Ом)
(Ом)
![]() (Ом)
(Ом)
![]() (Ом)
(Ом)
![]() (Ом)
(Ом)
5. Составим систему уравнений для двух контуров нашей цепи:
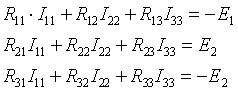
Подставим числовые значения и решим.
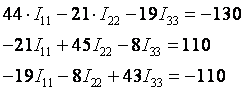
![]() (А)
(А)
![]() (А)
(А)
![]() (А)
(А)
Определим фактические токи в ветвях цепи:
![]() (А) направление совпадает с выбранным
(А) направление совпадает с выбранным
![]() (А) направление совпадает с выбранным
(А) направление совпадает с выбранным
![]() (А) направление совпадает с выбранным
(А) направление совпадает с выбранным
![]() (А) направление тока потивоположно выбранному
(А) направление тока потивоположно выбранному
![]() (А) направление совпадает с выбранным
(А) направление совпадает с выбранным
![]() (А) направление совпадает с выбранным
(А) направление совпадает с выбранным
6. Проверим баланс мощностей:
![]()
![]() (ВА)
(ВА)
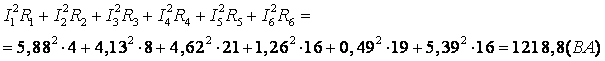 Небольшая разница в полученных результатах является результатом погрешности при округлении числовых значений токов и сопротивлений.
Небольшая разница в полученных результатах является результатом погрешности при округлении числовых значений токов и сопротивлений.
7. Построим потенциальную диаграмму контура изображенного на рис. 3. В качестве начальной точки примем узел 1.
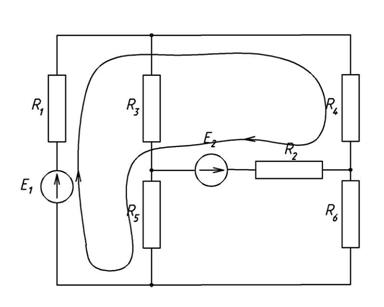
Рис.3
Для построения потенциальной диаграммы определим падения напряжения на каждом сопротивлении, входящем в выбранный контур.
![]() (В)
(В)
![]() (В)
(В)
![]() (В)
(В)
![]() (В)
(В)
Потенциал увеличивается если обход осуществляется против направления тока, и понижается если направление обхода совпадает с направлением тока. На участке с ЭДС потенциал изменяется на величину ЭДС. Потенциал повышается в том случае, когда переход от одной точки к другой осуществляется по направлению ЭДС и понижается когда переход осуществляется против направления ЭДС.
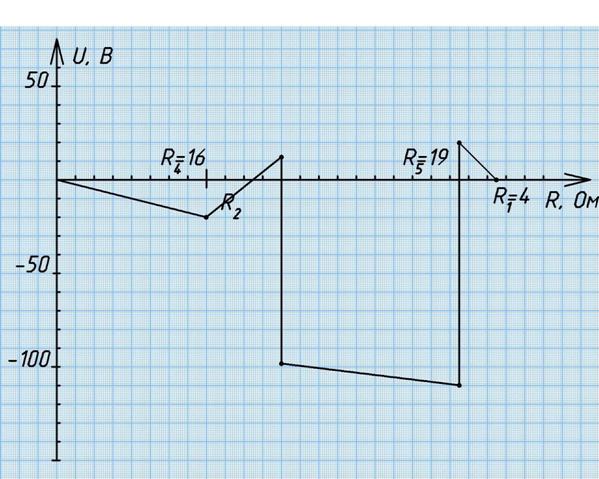
Рис. 4. Потенциальная диаграмма. ЗАКАЗАТЬ РАБОТУ!
Решить онлайн! (New!!!)


